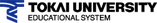At present we perform research in the following two fields: The quark structure of hadrons, and the physics of many-body systems. These researches are performed in collaboration with Argonne National Laboratory (Physics Division), the University of Adelaide (CSSM) and RIKEN (RNC). They were partially supported by a Grant of the Japanese Ministry of Education, Culture, Sports, Science, and Technology .
Ⅰ. The quark structure of hadrons
The research field of our group is hadronic and nuclear physics. We use effective quark theories of QCD to describe the internal structure of hadrons, nuclei, and neutron stars.
Here we introduce two of our recent research topics.
(1) Motion of quarks in hadrons:
Fig.1 shows the momentum distribution of quarks inside a vector meson. These distributions will be measured at the electron-ion collider in the US, where high energy electrons are scattered off hadrons. The two variables in Fig.1a are the longitudinal momentum fraction (x) and the square of the transverse momentum (kT2) of the quark. Fig.1b shows the results obtained by integrating over the transverse momentum components of the quarks, i.e., the PDF(=Parton Distribution Functions). The 4 lines in this figure correspond to different spin directions of the meson (spin 1) and the quark (spin 1/2). (From: Y.Ninomiya, W.Bentz, I.C. Cloet: Phys. Rev. C 96, 045206(2017).)
(2) Nuclear response functions:
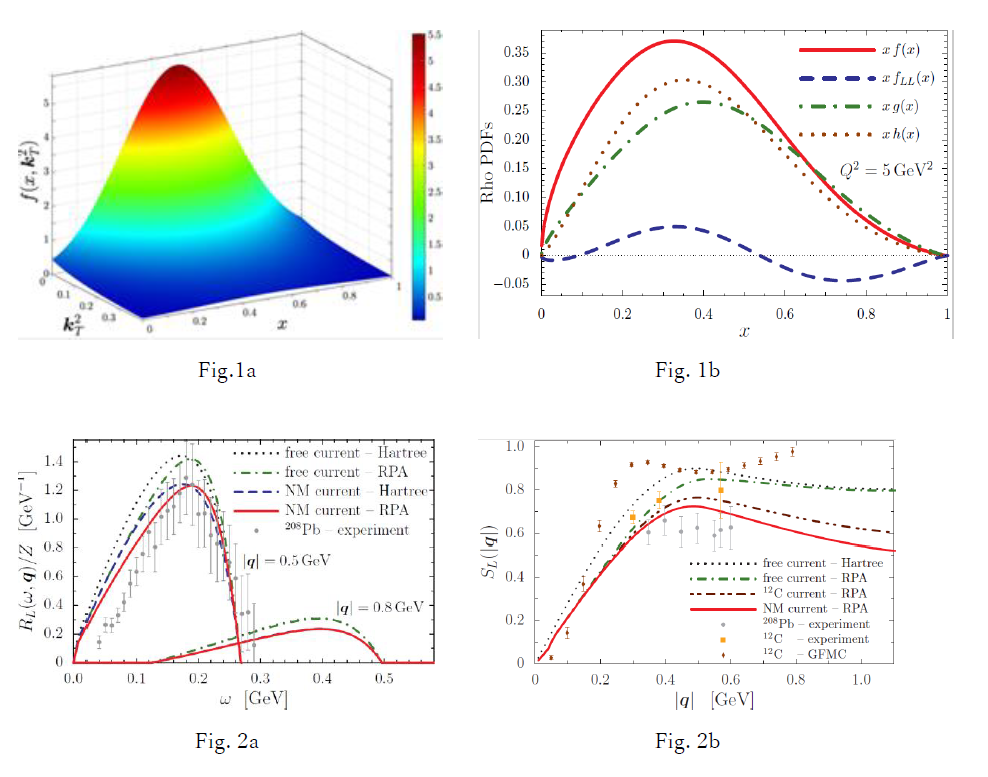
Fig.2a shows the Coulomb response fuction for inelastic electron scattering on a heavy nucleus (lead target). The variable ω is the enegy transfer, and q is the momentum transfer. The solid line includes effects of nuclear interactions and the medium (change of quark motion in a nucleus), and can be compared to the experimental data for a lead taget. Fig.2b shows the results obtained by integrating over the energy transfer, i.e., the Coulomb sum rule. The solid line includes effects of nuclear interactions and the medium, and can be compared to the experimental data for a lead target. (From: I.C. Cloet, W.Bentz, A.W. Thomas, Phys. Rev. Lett. 116, 032701(2016).)
Ⅱ. Many body systems
In our recent research on many body systems, we concentrated on the equation of state of nuclear matter at high baryon densities, the phase transition to quark matter, and the structure of compact stars.
In our previous works we constructed the nuclear matter equation of state by taking into account the quark substructure of the nucleons, and investigated the phase transition to color superconducting quark matter at high densities. One important result of these studies was that the long-standing problem of the "chiral collapse" of nuclear matter is solved when the confinement of quarks is taken into account.
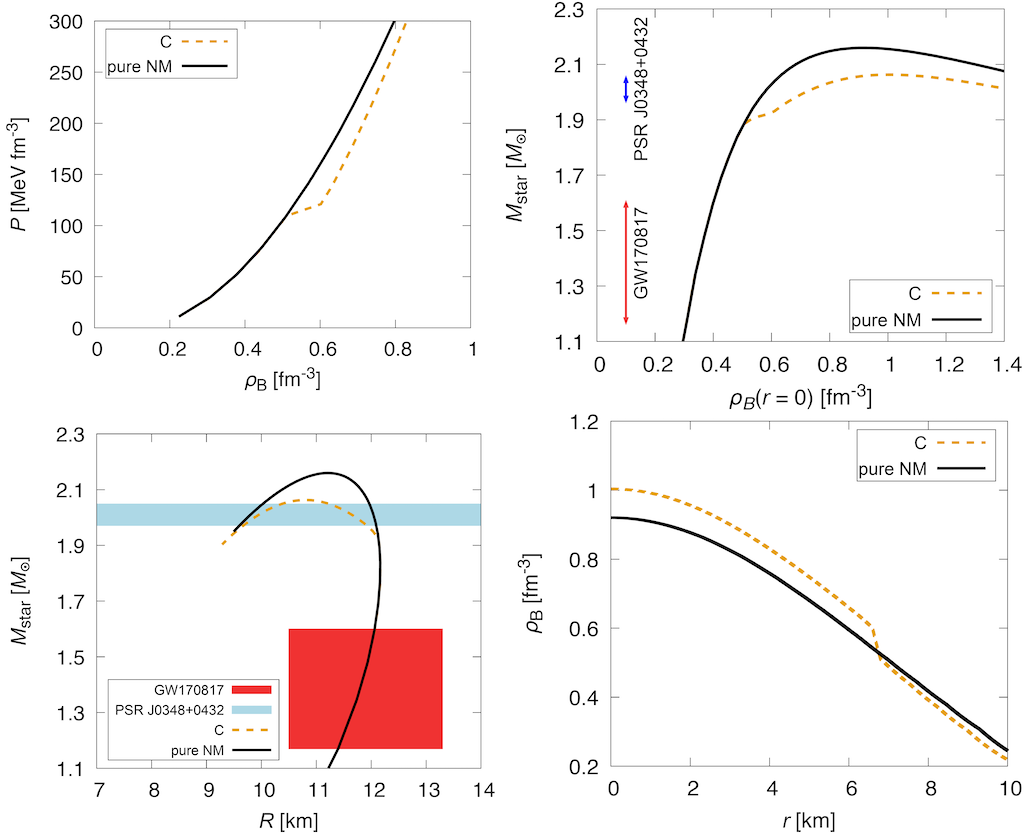
we extended these studies to the case of isospin asymmetric matter in beta equilibrium, and used the resulting equation of state to investigate the structure of compact stars. The figure below shows an example of
our results.
The left top figure shows the equation of state for pure nuclear matter (NM), for the transition to color superconducting quark matter (SQM).
The right top figure shows the resulting neutron star masses as functions of the central density,
the left bottom one shows the relation between the star masses and radii,
and the right bottom figure shows the profiles of the stars with the maximum mass. From the last figure, we see that in this scenario, a neutron star with 2.07 solar masses consists of QM (including a thin shell of NM-QM mixed phase) within a large radius of about 6.9 km. (From: T.Tanimoto, W.Bentz, I.C. Cloët. Phys. Rev. C101 (2020), 055204 (1903.06851)
Tokai University, Department of Physics, School of Sience
Professor Wolfgang Bentz